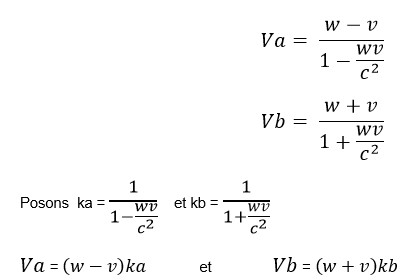Dès 1905, Albert Einstein avec la relativité restreinte mit fin à la simultanéité des évènements entre repères se déplaçant l’un par rapport à l’autre. Par exemple, si l’allumage de deux voyants lumineux L1 et L2 est simultané pour Alice, pour Bob qui se déplace vers la droite d’Alice, L1 s’allume avant L2. Pour Charly qui se déplace vers la gauche d’Alice, c’est L2 qui s’allume avant L1. On notera au passage que la notion de présent se dissout avec celle de simultanéité : le présent pour Alice diffère de celui de Bob, qui diffère de celui de Charly. Dans la majorité des démonstrations sont utilisés des signaux lumineux, donc de vitesse c invariante quel que soit le référentiel. Certes, cette approche facilite l’explication de la perte de simultanéité, comme on le verra ci-dessous. En même temps il est légitime* de se poser la question : ce phénomène persiste-t-il pour les objets matériels, c’est-à-dire quand la vitesse est inférieure à celle de la lumière ? On montrera que c’est le cas par la suite.
La relativité de la simultanéité avec la lumière
Un wagon se déplace vers la droite à la vitesse w par rapport à l’observateur O immobile sur le sol de la voie ferrée (on oublie les personnages ci-dessus).
VUE DU TRAIN en P
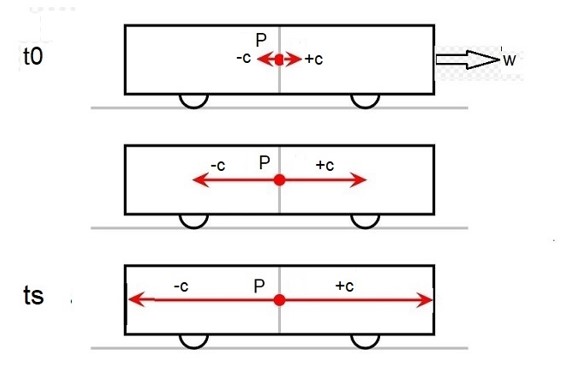
Le passager P assis au milieu du wagon émet deux signaux lumineux de sens opposés au même instant parallèles à la voie.
Pour P, les faisceaux atteignent les deux extrémités du wagon simultanément, c’est-à-dire au même instant ts selon l’horloge du wagon.
VUE DU SOL en O
La vitesse de la lumière c est constante, indépendante de la vitesse de la source. En conséquence le rayon dirigé vers la gauche atteint la paroi gauche qui vient à sa rencontre à t1 avant que le rayon dirigé vers la droite ne rattrape la paroi droite du wagon à t2.
Comme t1 # t2, il n’existe plus de simultanéité.
La relativité de la simultanéité avec des projectiles
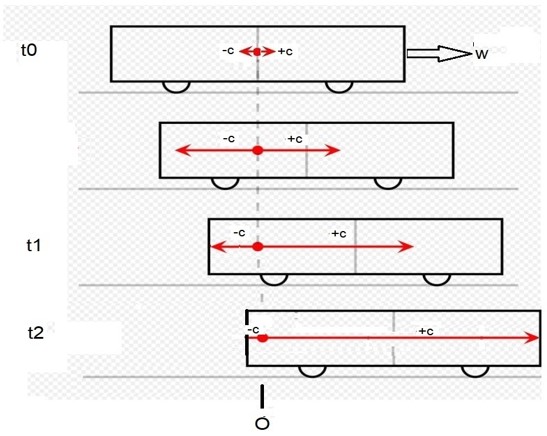
Cette fois le passager P lance deux pierres identiques à l’instant t0 : la pierre A vers l’arrière du wagon à la vitesse –v et la pierre B vers l’avant à la vitesse +v par rapport au wagon.
En physique Newtonienne, les vitesses s’additionnent et, vu du sol, pour l’observateur O
Pour A Va = w – v
Pour B Vb = w + v
Ce qui garantit l’arrivée simultanée des pierres A et B sur les parois, aussi bien pour l’observateur au sol O que pour le passager du train P.
A va moins vite que le wagon mais la paroi gauche vient à sa rencontre. B va plus vite que le wagon, mais elle doit rattraper la paroi droite.
En relativité restreinte
On constate encore la perte de la simultanéité, comme dans le cas des rayons lumineux. La pierre A atteint la paroi gauche avant que la pierre B n’atteigne la paroi droite. La raison en est une nouvelle cinématique propre à la relativité (voir l’annexe).
La loi de composition des vitesses n’est plus une simple addition comme chez Newton, elle fait intervenir la constante c, vitesse de la lumière (voir le calcul en annexe).
Comme ka > 1 et kb < 1 en relativité on constate que les vitesses composées comparées au cas Newtonien sont
– Va supérieure,
– Vb inférieure.
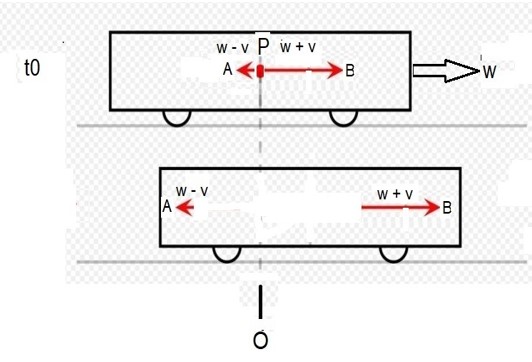
La pierre A arrivera avant la pierre B sur leur paroi réciproque.
Le « présent » du passager P, c’est dire l’impact simultané de A et B diffère du « présent » de l’observateur O au sol puisque celui-ci observe d’abord l’impact de A puis l’impact de B.
En annexe
Calcul de la formule de composition des vitesses en relativité voir (PDF joint)
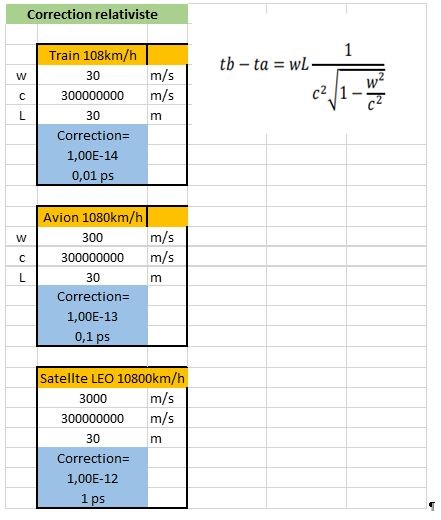
Calcul des différences de temps
Même pour un satellite, le décalage n’est que de 1 pico seconde
*Référence « Déjouez les idées fausses en physique » Pierre Spagnou , Ellipses 2017
Ph Loutrel, A Bertout www.loutrel.org